Bestimmung von e/m (e/m)

Graphen

1 Grundlagen und Versuchsdurchführung

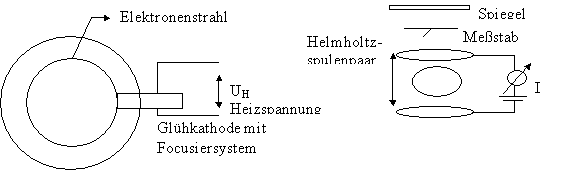
Man kann das Verhältnis von e/m bestimmen, in dem man die Ablenkung eines Elektronenstrahls in einem angelegten Magnetfeld betrachtet. Dazu verwendet man ein Fadenstrahlrohr. Es erzeugt durch eine Heizspannung thermische Elektronen die dann durch eine angelegte Spannung beschleunigt werden. Die Geschwindigkeit kann dadurch errechnet werden das die Elektronen eine vernachlässigbare Anfangsgeschwindigkeit haben und danach genau die Energie U*d (d = Weglänge im Feld) in kinetische Energie umwandelt. So beschleunigt werden die Elektronen senkrecht in ein homogenes Magnetfeld geschossen.

Dieses Magnetfeld wird durch ein Helmholtz Spulenpaar erzeugt, welches zwischen den Spulen ein nahezu homogenes Magnetfeld erzeugt. Um den Elektronenstrahl sichtbar zu machen, wird der ganze Vorgang in einem abgeschlossenem Kolben, der mit Wasserstoff unter 1,3 bar gefüllt ist, durchgeführt.

Der Elektronenstrahl wird durch das Magnetfeld auf eine Kreisbahn gebracht. Haben die Elektronen in Richtung des Magnetfeldes keine Geschwindigkeitskomponente, so bilden sie einen Kreis. Andernfalls entsteht eine Schraubenlinie, die man durch vorsichtiges drehen des Kolbens, also leichte Änderung der Einschußrichtung, zu einem Kreis machen kann.

Mit zu Hilfenahme einer sogenannten Wehnert Spannung kann man erreichen, daß der Elektronenstrahl gebündelt ist und nicht divergiert, wobei durch ausprobieren im Bereich -25 - 0 V erhält man die gewünschte Bündelung.

Man mißt parallaxenfrei den Durchmesser des Elektronenstrahlkreises indem man den höchsten und tiefsten Punkt des Kreises mit dem Spiegelbild in dem dahinter gestellten Spiegels zur Deckung bringt und so die Höhendifferenz = Durchmesser am aufgestellten Lineal mißt. Da der Strahl sehr diffus war, war es sehr schwierig das Spiegelbild und den realen Strahl zur Deckung zu bringen, welches unseren Meßfehler nochmals vergrößert hat.

Für 5 verschiedene Werte der Beschleunigungsspannung (150, 180, 210, 240, 300 V) haben wir jeweils 5 mal den Durchmesser des entstandenen Kreises wie oben beschrieben gemessen.

2 Versuchsauswertung

Zum Ablesen wurde von uns nur die Millimeterskala verwendet, nicht der Nonius, da das „Flackern“ des leuchtenden Kreises Abweichungen während der Messung in höherer Größenordnung bewirkte.

Zusätzliche Anmerkungen: Abweichung bei der Höhenmessung: ± 0,0005

Rechnungen siehe Protokollheft.

Als Endergebnis habe ich e/m=(171±6) 10⁹ C/kg erhalten.

In der Literatur findet sich ein Wert von 175 10⁹ C/kg, was erfreulicherweise trotz des hohen Meßfehlers wegen der Divergenz im Bereich des erhaltenen Meßergebnisses liegt.

3 Fragen

3.1

Man beschleunigt Elektronen, z.B. wieder durch ein elektrisches Feld, und läßt sie nun in ein zur Bewegungsrichtung quer gerichtetes E-Feld durchfliegen. Es wirkt eine Kraft auf das Elektron, das aber je nach Größe der beschleunigten Masse zu unterschiedlichen Beschleunigungen führt (aufgrund der Masseträgheit). Aus der Ablenkung am Ende des Feldes kann so e/m errechnet werden.

3.2

Es ergibt sich dann kein Kreisbahn, sondern eine Bahn in Form einer Spirale (Helix). Dies kann dadurch rechnerisch gezeigt werden, indem man den Geschwindigkeitsvektor in 2 Komponenten zerlegt: die erste, die senkrecht zum B-Feld steht, die zweite, die parallel zum B-Vektor steht. Nur die erste Komponente trägt zur Lorentzkraft bei, während die Bewegung in Richtung der zweiten Komponente unverändert konstant bleibt.

3.3

Die beschleunigten Elektronen regen das Wasserstoffgas auf ihrer Flugbahn durch Stoßprozesse zum Leuchten an, das Gas steht unter geringem Druck, um eine geringe Dichte des Gases und damit eine überschaubare Anzahl von Stoßprozessen zwischen Elektronen und Gasmolekülen zu gewährleisten (bei zu vielen Stößen würde die "Leuchtspur" zu kurz für Messungen).

3.4

Das Erdmagnetfeld läßt sich in zwei Komponenten teilen, eine senkrecht zu den Helmholtzspulen und eine parallele. Die Parallele zieht den Kreis zu einer Spirale auseinander, verändert aber nicht dessen Radius, ist also für uns nicht von Bedeutung. Die senkrechte Komponente verstärkt oder schwächt das von den Helmholtzspulen erzeugt Feld und bewirkt dadurch eine Änderung des Radiuses, welchen wir messen könnten und welcher unsere Messungen beeinträchtigen könnte. Um dieses Feld nachzuweisen, müßte man die Apparatur drehen und den maximalen bzw. minimalen Radius bei gleichbleibender Spannung finden. Aus dieser Differenz läßt sich dann der Betrag der senkrechten Komponenten finden. Das Erdmagnetfeld liegt bei ca. 3*10^-5 T, es zeigt sich nach einfacher Überlegung, daß hier Abweichungen im Radius von weit unter einem Millimeter gemessen werden müßten, dies ist in Anbetracht der Meßungenauigkeit schlichtweg unsinnig.

3.5

Zur rechnerischen Auswertung siehe Sektion 2.