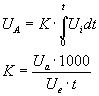Messung der Hystereseschleife (HYS)

Graphen

Integratoreichung und Eisen
Eisen klein
Ferrit
Ferrit klein
4.5

1 Eichung des Integrators

Als erstes muß für alle späteren Versuche der Integrator geeicht werden. Um keine Temperaturdrift zu erhalten, muß man das Gerät vorher ungefähr 10 Minuten warmlaufen lassen. Danach legt man am X-Eingang des XY-Schreibers eine konstante Spannung an. Der 1000-te Teil dieser Spannung wird nun auch auf den Integrator gelegt. Man startet den XY-Schreiber und beläßt die Eingangsspannung 60 Sekunden lang. Um später mit 2 Meßwerten rechen zu können, haben wir noch die Spannung umgepolt und den Versuch wiederholt.

1.1 Berechnung des K-Faktors

Mit der erhaltenen Kurve kann man so den K-Faktor berechnen:
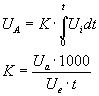U_a Spannung vom Integrator; U_e Spannung von Spannungsquelle

gemessene Werte:
1. U_e = 14,0 V , U_a = 12,4 V; t = 60 s => K = 14,76 1/s
2. U_e = 13,9 V , U_a = 12,4 V; t = 60 s => K = 14,87 1/s
Wir erhielten damit für K zwei fast identische Werte und haben danach mit K = 14,8 1/s weitergerechnet.

2 Messung der Hysteresekurve von Weicheisen

2.1 Versuchsaufbau

Als nächstes haben wir die Hysteresekurve von Weicheisen gemessen. Dazu stellten wir folgenden Versuchsaufbau her:

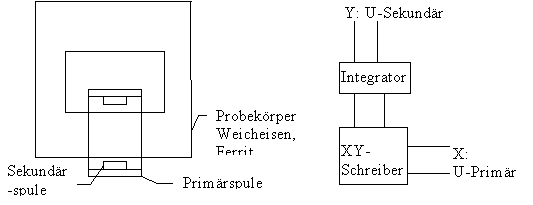
Um eine Neukurve zeichnen zu können, muß zuerst der Probekörper entmagnetisiert werden. Dies kann dadurch erreicht werden, indem man die Hystereseschleife mit immer geringerem H durchfährt. Damit läßt sich theoretisch die Entmagnetisierung zwar nicht vollkommen erreichen, da immer eine kleine Remanenz beibehalten wird, aber praktisch ist er fast entmagnetisiert.

Nun mußten wir noch einen Nullpunkt einstellen und das dazugehörige Koordinatensystem einzeichnen. Danach haben wir mit der entmagnetisierten Probe die Hysteresekurve neu durchfahren, wobei wir bis zur maximalen Stromstärke von 1,75 A gegangen sind.

2.2 Versuchsauswertung:

Die Hysteresekurve ist zu den eingezeichneten Koordinatenachsen nicht ganz punktsymmetrisch, wie sie es eigentlich im Idealfall sein müßte. Dies kommt daher, daß sich der Probekörper trotz der oben erwähnten Behandlung nicht ganz entmagnetisiert hat. Wir haben die Achsen dadurch zentriert, daß wir bei der Messung der Spannung für die Remanenz und Sättigung beide Werte der Kurve, d.h. oben/unten bzw. links/rechts, gemittelt haben.

Aus der aufgezeichneten Kurve haben wir folgende Spannungswerte entnehmen können:

	U (B) [V]	U (B_r) [V]	U (H_s) [V]	U (H_c) [V]
U(1)	8,2	2,4	2,10	0,22
U(2)	7,8	2,4	2,04	0,22
U (mittel)	8,0	2,4	2,07	0,22

Dadurch kann man mit:

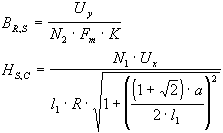
U_y: Spannung am Integrator;
N₁ N₂: Wicklungen Primär-/Sekundärspule (100/2000);
l₁: Länge der Primärspule (0.034m);
a: Spulenöffnung (0.020 m);
F_m: Querschnittsfläche der Probe
(Weicheisen: 3,52*10^-4m², Ferrit: 1.96*10^-4 m², AlNiCo: 1,80*10^-4 m²);
K: Integrationsfaktor (14,8 1/s);´
R: U_max/I_max = V / 1,75 A = 1,2 W

die magnetische Feldstärke der Primärspule und den magnetischen Fluß der Probe errechnen.

Als Werte erhielten wir

Stoff	Induktion B [Vs/m²]	Remanenz B_r [Vs/m²]	Sättigung H_s [A/m]	Koerzitiv H_c [A/m]
Weicheisen	0,769	0,231	4137	440
Ferrit	0,431	0,034	4137	60
Dauermagnet		0,019

3 Hystereseschleife eines Ferritkernes

Den selben Versuch haben wir nun auch für eine Ferritprobe ausgeführt. Da die Hysteresekurve jedoch viel enger an der y-Achse liegt, haben wir, um die Remanenz genauer bestimmen zu können, die Auflösung des XY-Schreibers erhöht. Wir errechneten aus:

	U (B) [V]	U (B_r) [V]	U (H_s) [V]	U (H_c) [V]
U (1)	2,5	0,2	2,08	0,03
U (2)	2,5	0,2	2,06	0,03
U (mittel)	2,5	0,2	2,07	0,03

mit denselben Formeln die Daten für Induktion, Remanenz, Sättigung und Koerzitivfeldstärke. Die Werte haben wir auch in die vorherige Tabelle geschrieben.

4 Messung der Remanenz eines Dauermagneten

Um die Remanenz eines Dauermagneten zu messen, mißt man im Endeffekt die in die Sekundärspule induzierte Spannung.

Wir erhielten einen Wert von:
U(ind) = 0,1 V

Nach Einsetzen in die obigen Formeln kann man so wieder die Remanenz errechnen:
B_r = 0,019 Vs/m²

5 Fragen:

5.1

Ferromagnetismus kann dann auftreten, wenn der Stoff schon „Elementarmagnete“ (größere Bereiche in denen die Spins der Elektronen parallel zueinander ausgerichtet sind) besitzt. Diese magnetischen Dipole müssen schon untereinander stark wechselwirken und sich in gewissen Bezirken („Weiß’schen Bezirke“) gleich ausrichten.

5.2

Im entmagnetisierten Material sind, obwohl kein äußeres Feld mehr existiert dennoch Weiß’sche Bezirke vorhanden. Sie sind statistisch verteilt und kompensieren sich nach außen hin jedoch so, daß kein Feld nach außen entsteht.

5.3

Ein Sättigungswert ist dann erreicht, wenn sich alle Bezirke genau nach dem Feld ausgerichtet haben. Wenn man dennoch die Feldstärke weiter erhöht, bleibt die Magnetisierung J konstant.

5.4

Es kommt zu einer Hysteresekurve, da die magnetischen Dipolmomente auch nach Erniedrigung der äußeren Feldstärke dennoch nicht alle in ihre vorige Position zurückfallen, sondern immer noch in Teilbezirken gleich ausgerichtet bleiben. Das heißt der Stoff wird auch nach Abschalten des äußeren Feldes nicht vollständig entmagnetisiert. Dadurch geht der magnetische Fluß nicht in dem Maße zurück wie die äußere Feldstärke und es bildet sich die Hysteresekurve.

5.5

Für magnetisch weiche Materialien ist die Hysteresekurve schmal (z.B.: Ferrit). Das heißt, es ist wenig Arbeit notwendig, um sie umzumagnetisieren. Für magnetisch harte Materialien ist die Hysteresekurve breit (z.B.: „Weicheisen“, Permanentmagnet (sehr hart)) und somit benötigt man mehr Arbeit.

5.6

Magnetisch harte Substanzen eignen sich zur Herstellung von Dauermagneten. Sie können das einmal geschaffene Magnetfeld lange behalten, da die äußeren Störungen sehr groß sein müssen, um sie zu entmagnetisieren. Sie eignen sich somit für Dauermagnete, wie sie auch in Lautsprechern eingesetzt werden. Magnetisch weiche Substanzen eignen sich dann, wenn sie oft umgepolt werden müssen. Daher eignen sie sich vor allem für Transformatoren und Hochfrequenztechnik.

5.7

Die durch Temperaturunterschiede im Integrator entstehende Drift der y-Achse hat zur Folge, daß man beim mehrmaligen Durchlaufen der Kurve unterschiedliche Werte für die Sättigungsspannung erhält. Die Drift hat auch zur Folge, daß sich der Werte der Remanenz verschiebt. Eine weitere Fehlerquelle ist auch die Integrationskonstante, die nicht notwendigerweise konstant ist.

5.8

Da Luft ein Dielektrikum ist, würde sich die Induktion B verringern. H(c) und H(s) würde größer werden, d.h. man müßte den Strom erhöhen. B(Sättigung) und B(Remanenz) bleiben gleich, da die Luft keine Remanenz hat. Der Fläche zwischen der Kurve wird größer, da man mehr Energie aufbringen muß um die Sättigung zu erreichen. Durch den Luftspalt sind weniger magnetisierbare Momente pro Volumeneinheit vorhanden, und somit wird sich k und m erniedrigen.