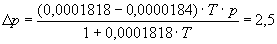Bestimmung der molaren Masse (MOL)

1 Grundlagen

Der Methode zur Bestimmung der molaren Masse nach Dumas liegt die allgemeine Zustandsgleichung idealer Gase zugrunde. Ein ideales Gas ist im Prinzip nur eine Modellvorstellung für theoretische Untersuchungen über das Verhalten von Gasen. Vor allem wird das Eigenvolumen der Moleküle, sowie alle Wechselwirkungen außer elastischen Stößen zwischen ihnen vernachlässigt. Nur auf diese Weise erfüllt ein Gas die erwähnte Zustandsgleichung

pV = nRT

R=8,3143 J K mol^-1: Gaskonstante, p: Druck, T: Temperatur, V: Volumen des Gases, n: Stoffmenge des Gases in Mol. Ersetzt man die Stoffmenge n = m/M, so kommt man auf die Formel

M = mRT/pV

mit der man die molare Masse bestimmen kann. Bei der Methode von Dumas werden von diesen Versuchsvariablen V, p und T durch die Umgebungsbedingungen gegeben. Die Eigenschaften realer Gase nähern sich denen eines idealen Gases um so mehr an, je geringer der Druck und je höher die Temperatur ist, also d.h. je weiter die Bedingungen des Gases von seinem Kondensationspunkt entfernt sind.

Um nun die molare Masse von Chloroform zu bestimmen, wird ein wenig Chloroform in einen Glaskolben gesogen, der dann in einem Wasserbad erhitzt wird, bis das Chloroform bei der Temperatur T und dem Druck p verdampft. Um T möglichst genau zu bestimmen, wird für den vorherrschenden Druck die Siedetemperatur des Wassers ermittelt, welcher auch dann zugleich die Temperatur des Chloroforms im Kolben ist. Damit das Eindringen von fremden Gasen verhindert wird, befindet sich das Ende der Kolbenkapillare in flüssigem Chloroform. Die Kapillare wird abgeschmolzen, sobald der Kolben nur noch gasförmiges Chloroform enthält. Die Masse wird somit durch Wägung bestimmt, während man das Volumen erhält, indem man den Kolben mit Wasser füllt und ihn dann abermals wiegt.

2 Auswertung des Versuches

Zuerst wurden die Umgebungsbedingungen, d.h. der barometrische Druck und die Raumtemperatur festgehalten:

p’ = (727,5 ± 0,5) Torr

T = 21,0 °C ± 0,1 °C = 294,0K ± 0,1K

Da das Barometer auf 0° C geeicht ist, muß der Druck um einen Faktor korrigiert werden.

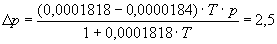Torr

p = p’ - Dp= 725 ± 0,5 Torr = 96660 ± Pa.

Der korrigierte Siedepunkt von Wasser bei diesem Druck ist aus der Tabelle entnommen

T_s= 98,685 °C = 371,84 K

Um die molare Masse des Chloroforms zu bestimmen, wurden folgende Massen des gefüllten Glaskolbens gemessen:

m_Luft = m_L = 17,557 ± 0,001 g

m_HCCl3 = m_C = 17,822 ± 0,001 g

m_H2O = m_W = 117,267 ± 0,001 g

Wir fassten alles zu einer Formel zusammen:

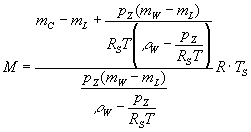= 116 ± 1

3 Anmerkungen zur Fehlerrechnung:

Da 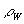>> 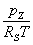ist, kann der Fehler dieses Terms vernachlässigt werden.

Nach partieller Differenzierung nach m_C, m_L, m_W, p_Z, T und Anwendung der Formel 7 (ABW Seite 10) des Skripts kommt man auf den obengenanten Fehler.

Nicht berücksichtigen konnten wir die etwaigen auftretenden systematischen Fehler bei der Gewichtsmessung, sowie beim Abschneiden des Glasröhrchens wegfallende Splitter.

Den restlichen Fehler kann man dadurch erklären.

4 Fragen

4.1

Als Stoffmenge wird eine bestimmte Anzahl von Teilchen bezeichnet. Ihre Einheit ist das Mol. Ein Mol eines Stoffes enthält ebenso viele Teilchen, wie sich Atome in 12 g Kohlenstoff (¹²C) befinden. Diese Menge Kohlenstoff enthält genau 6,022 10²³ Atome, wodurch die Anzahl der Teilchen eines Stoffes in einem Mol festgelegt ist. Diese Konstante wird Avogadro Konstante genannt: N_A= 6,022 10²³ mol ^-1.

4.2

Als molare Masse wird die Masse von einem Mol eines bestimmten Stoffes bezeichnet: M=m/n=[kg/mol]. Die relative Molekülmasse gibt an, um wieviel größer die Masse eines Moleküls im Vergleich zu einem Zwölftel der Masse eines Atoms des Kohlenstoffisotops ¹²C ist. Betrachtet man keine Isotopengemische, so stimmt die molare Masse in g/mol mit der relativen Atommasse im Zahlenwert überein.

4.3

Befindet sich in gleichem Volumen bei gleichen Druck und Temperatur dieselbe Stoffmenge zweier verschiedener Gase, so muß nur die Stoffmenge eines der beiden Gase im idealen Zustand bekannt sein. Dann muß man nur noch das zu messende Gas in denselben Zustand versetzen, wobei man seine Stoffmenge kennt. Es muß noch die Masse bestimmt werden (z.B. durch einfaches abwiegen). Bei bekannter molarer Masse eines Gases gilt im selben Zustand: n₁=n₂ => M₁m₂/m₁=M₂.

4.4

Die Methode von Dumas ist nur für Stoffe geeignet, die bei Raumtemperatur flüssig sind und unter der Siedepunktstemperatur von Wasser verdampfen. Auch sollte der verdampfte Stoff sich wie ein ideales Gas verhalten, denn diese Methode baut auf dem Gasgesetz für ideale Gase auf. Das zu untersuchende Gas sollte also nicht unter zu starken Druck stehen und die Gasmoleküle sollten keine zu starken Wechselwirkungen aufeinander zeigen. Das Gas sollte auch beim verdampfen nicht dissoziieren. Für Festkörper ist diese Methode ungeeignet.

4.5

Mit dem Massenspektrographen läßt sich die relative Molekülmasse feststellen und damit auch die molare Masse. Bei bekanntem Dissoziationsgrad eines in Lösung gegangenen Stoffes kann über die Gefrierpunktserniedrigung oder Siedepunktserhöhung die molare Masse bestimmt werden. Auch die Elektrolyse eignet sich dafür, denn durch die transportierte Ladung läßt sich die Menge der an den Elektroden angelagerten Moleküle bestimmen. Die Masse kann dann durch abwiegen bestimmt werden.