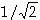 Teil der Spannung im Resonanzfall gedämpft wird. Die Güte gibt das Verhältnis zwischen der
Resonanzfrequenz und der Intervalllänge an, und ist ein Maß für die Wirkung
des Schwingkreises.
Teil der Spannung im Resonanzfall gedämpft wird. Die Güte gibt das Verhältnis zwischen der
Resonanzfrequenz und der Intervalllänge an, und ist ein Maß für die Wirkung
des Schwingkreises.Schwingkreis
Tiefpaß
Phasenverschiebung über Frequenz
Im Gegensatz zu normalen Spannungsmessern kann der Oszillograph die zu messenden Spannungen graphisch anzeigen. Dadurch kann zum Beispiel auch eine Phasenverschiebung sichtbar gemacht werden. Ein weiterer Vorteil besteht darin, daß durch die geringe Trägheit auch hochfrequente Spannungen gemessen werden können.
Zuerst wird durch eine Kathode ein Elektronenstrahl in der evakuierten Röhre erzeugt, der dann später gebündelt wird (Durchlauf durch „Plattenkondensator“-Paare, die angelegte Spannung bewirkt ein E-Feld, durch das dann die Elektronen in x bzw. y-Richtung abgelenkt werden. Normalerweise wird an das eine Paar eine Spannung angelegt, so daß die x-Richtung linear in der Zeit ist. Danach prallen die Elektronen auf den Schirm auf, der durch eine Lumineszenzschicht (z.B. Phosphor) ein Leuchten erzeugt. So erhält man ein t-U-Diagramm.
Wichtig ist auch noch die sogenannte Triggerung der Eingangsspannung, damit auf dem Schirm eine stehendes Bild entsteht. Dies geschieht dadurch, daß die Zeitablenkspannung nach dem Rücklauf erst wieder einsetzt, wenn die zu messende Spannung einen bestimmten einstellbaren Wert unter- oder überschreitet.
Der Serienschwingkreis dient dazu, nur eine gewisse Bandbreite durchzulassen, während alle anderen Frequenzen herausgefiltert werden.
Charakteristisch für einen
Schwingkreis ist vor allem die Resonanzfrequenz (d.h. die Frequenz, für die
die Ausgangsspannung maximal wird), die Bandbreite und die Güte. Die
Bandbreite ist ein Frequenzintervall, indem die Ausgangsspannung höchstens
auf den 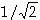 Teil der Spannung im Resonanzfall gedämpft wird. Die Güte gibt das Verhältnis zwischen der
Resonanzfrequenz und der Intervalllänge an, und ist ein Maß für die Wirkung
des Schwingkreises.
Teil der Spannung im Resonanzfall gedämpft wird. Die Güte gibt das Verhältnis zwischen der
Resonanzfrequenz und der Intervalllänge an, und ist ein Maß für die Wirkung
des Schwingkreises.
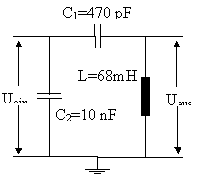
Der Versuch wurde wie auf der nebenstehenden Skizze aufgebaut. Die sinusförmige Eingangsspannung wurde von einem Frequenzgenerator (FG) erzeugt, bei dem stufenlos die Frequenz eingestellt werden konnte. Der Ausgang wurde mit der Eingangsspannung auf den Oszillographen gelegt.
Zuerst bestimmten wir die Resonanzfrequenz, indem wir den Maximalausschlag der Spannung auf dem Oszillographen suchten, und dann die Frequenz vom FG ablasen.
Danach maßen wir bei verschiedenen Frequenzen die Ausgangsspannung um später eine Durchlaßkurve zu erhalten.
Die Resonanzfrequenz läßt sich nicht nur durch den
Versuch bestimmen, sondern auch durch eine theoretische Rechnung:
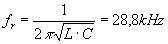
wobei C die Gesamtkapazität der Reihenschaltung aus C1
und C2 ist.
Während wir bei der Messung der Resonanzfrequenz eine
Wert von
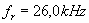
gemessen haben. Der Unterschied dieser beiden Werte ergibt sich wohl hauptsächlich aus den
kapazitiven und ohmschen Widerständen von Kabeln und Meßgeräten. Die
gemessene Durchlaßkurve haben wir in ein f-U Diagramm eingezeichnet und mit
einer Kurve extrapoliert. Daraus haben wir dann die Bandbreite bestimmt, indem
wir die Maximalspannung durch 21/2 geteilt haben und so den
Schnittpunkt an der f-Achse bestimmt. Die Güte erhält man, indem man die
Resonanzfrequenz durch die Bandbreite teilt:
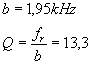
Um genauer die
Resonanzfrequenz des Schwingkreises zu bestimmen, verwendet man einen
Tastkopf. Um die Wirkung des Tiefpasses im Oszillographen auszugleichen, ist
im Tastkopf ein Kondensator eingebaut, der wie ein Hochpaß wirkt. Um ihn auf
dieselbe Grenzfrequenz wie den Tiefpaß im Oszillographen zu bringen, wird der
Drehkondensator im Tastkopf mit einem kleinem Schraubenzieher geeicht, so daß
eine im Oszilloskop erzeugte Rechteckspannung auch als solche angezeigt wird,
d.h. die Rechteckspannung ist nicht mehr an den Rändern verzerrt. Bei uns war
die voreingestellte Position bereits optimal. Wir erhielten eine
Resonanzfrequenz fr,T=25 kHz. Daraus läßt sich die Kapazität des
BNC Kabels bestimmen:
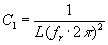
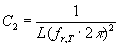
Die Differenz von C1
(Die Kapazität des Schwingkreises ohne Tastkopf) und C2 (Die
Kapazität des Schwingkreises mit abgeglichenem Tastkopf) ist dann genau die
Kapazität CBNC des BNC Kabels. In Unserem Fall ergibt sich
CBNC = C1 - C2 = 551 pF - 596 pF = -45 pF
Dies entspricht bei unserem Kabel der Länge 102 cm einer
Kapazität von -44 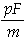 .
.
Dieser Wert erscheint uns sehr fraglich.
Der Tiefpaß dient dazu, ab einem bestimmten Frequenzwert alle darüberliegende Frequenzen herauszufiltern. Die gewünschte Ausgangsspannung wird am Widerstand abgenommen.
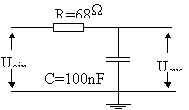
Als Eingangsspannung wurde der Frequenzgenerator verwendet und wieder mit der Ausgangsspannung auf den Oszillographen gelegt Danach wurden viele Frequenzen eingestellt und dann beide Spannungen, die Eingangs- und Ausgangsspannung gemessen.
Zusätzlich wurde die Phasenverschiebung, das heißt durch die Messung der Zeitdifferenz beim selben Schwingungsdurchgang, bei uns durch den Nullpunkt.
Um die Grenzfrequenz auch anders als durch die Kurve zu bestimmen, haben wir eine so niedrige rechteckige Spannung angelegt, so daß der Kondensator praktisch voll ent- bzw. aufgeladen war. Dadurch kann später durch Rechnung die Grenzfrequenz bestimmt werden.
Zuerst erstellten wir eine
f-U-Diagramm, bei dem wir auch näherungsweise die Grenzfrequenz eingetragen
haben. Das heißt die Frequenz, bei der die Spannung auf 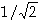 der Eingangsspannung abgesunken ist: fG = 24 kHz.
der Eingangsspannung abgesunken ist: fG = 24 kHz.
Danach errechneten wir durch:

ebenfalls die Grenzfrequenz: fG = 23.4 kHz.
(Dieser Wert weicht von dem graphisch ermittelten leicht ab, da
wir in dieser Gleichung nicht den Einfluß der Kabel und Geräte
berücksichtigen.)
Das Rechtecksignal wird bei
hohen Frequenzen in ein Dreiecksignal transformiert.
(TP: Integrationsglied)
Der Hochpaß ist dazu da, tiefe Frequenzen herauszufiltern und ab einer bestimmten Grenzfrequenz wieder durchzulassen. Dies geschieht dadurch, daß die Ausgangsspannung am Widerstand abgenommen wird, der dem Kondensator nachgeschaltet ist.
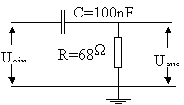
Der Hochpaß ist wie in der nebenstehenden Skizze aufgebaut. Da am Anfang der Versuchesdurchführung starke Probleme bei der Erzeugung einer sinusförmigen Ausgangsspannung am FG auftraten, was zu einer großen zeitlichen Verzögerung führte, wurde uns hier die entsprechende Veruschsreihe erlassen.
Wir erechneten die Grenzfrequenz durch
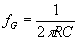 = 23,4 kHz
= 23,4 kHz
Das Rechtecksignal wird bei hohen Frequenzen zu einzelnen
Peaks (siehe Abb.17 Skript).
(HP: Differenzierglied)
Diese drei Bausteine können als Filter für bestimmte Frequenzbereiche verwendet werden. Je nach Anordnung dieser Bausteine wird dieser Frequenzbereich durchgelassen (Band-, Hoch-, oder Tiefpaß) oder gesperrt ( Bandsperre). Ein Schwingkreis läßt nur einen sehr engen Bereich durch, welcher durch die Güte des Schwingkreises bestimmt ist. Der Hoch- und Tiefpaß hingegen, läßt einen ganzen Bereich durch, genau der welcher über bzw unter der Grenzfrequenz des Passes ist. Diese Bausteine werden dazu verwendet, gewisse Frequenzen zu blockieren, welche als Störung wahrgenommen werden würden, wie etwa die 50 Hz des Haushaltsstroms. Sie spielen auch eine zentrale Rolle in der Unterhaltungselektronik (z.B.: Lautsprecher (HP, BP und TP in „Frequenzweichen“), Schwingkreis in der Antennentechnik etc. ).
| Mechanik | Elektrizitätslehre | ||
| Kraft von außen | FA | Eingangsspannung | U |
| Dämpfungsfaktor | G | Ohmscher Widerstand | R |
| Masse | m | Induktivität | L |
| Richtgröße | D | reziproke Kapazität | G |
| Auslenkung | x | Ladung des Kondensators | Q |
| Geschwindigkeit | v | Stromstärke | I |
| Beschleunigun | a | zeitliche Änderung von I | d2Q/dt2 |
Auch die Differentialgleichungen, anhand derer man die Schwingungen berechnen kann, sind gleich aufgebaut. Man muß lediglich die jeweils analogen Größen austauschen.
Bei hohen Frequenzen steigt der Widerstand der Induktivität, d.h. bei hohen Frequenzen steigt der Gesamtwiderstand des Schwingkreises an. Hohe Frequenzen werden also immer stärker gesperrt.