Der Kreisprozeß einer Stirling-Maschine ist, daß ein Gas verdichtet, geheizt, ausgedehnt und gekühlt wird, so daß es wieder im Grundzustand ist. Die beim Prozeß geleistete Arbeit wird auf ein Schwungrad übertragen. Wird es am Anfang angedreht, so liefert die gespeicherte Energie die Arbeit zum Verdichten des Gases und bei der Expansion erhält es die Arbeit plus der vom Kreisprozeß geleisteten Arbeit zurück, die Maschine arbeitet ohne äußeren Antrieb.
Die Thermodynamik des
idealisierten Gases stellt dabei die Verbindung zwischen Volumen, Druck und
Temperatur her. Beim idealen Gas gilt die Zustandsgleichung
pV = nRT
(p: Druck; V:
Volumen; n: Stoffmenge; T: Temperatur; R: Gaskonstante).
Ein mit der Stirling-Maschine verbundener Spiegel zeigt durch seine horizontale Auslenkung das in dem Kolben befindliche Volumen an, durch seine vertikale Auslenkung den herrschenden Druck. Ein Laserstrahl wird von ihm reflektiert und je nach Auslenkung an eine bestimmte Stelle der Wand, die mit Millimeterpapier bedeckt ist, geworfen.
Um die horizontale V-Achse bestimmen zu können klemmt man den Druckschlauch ab und bewegt den Kolben per Hand. Wegen der Reflexion wird die Achse immer ein bißchen gebogen bleiben. Die Volumendifferenz beträgt nach Angabe des Herstellers 150 ± 0,5 cm³.
Danach muß eine Druckskala auf dem Papier eingezeichnet werden. Dazu pumpt man Luft mit einer Luftpumpe in den Kolben und schließt zur Druckmessung ein Manometer an und trägt den gemessenen Druck auf der Skala ein.
Zuerst wird die Stirling-Maschine als Motor verwendet.
Dazu legt man eine Heizspannung, die durch einen Trafo erzeugt wird, an die Heizwendel im oberen Teil des Kolbens. Nachdem die Wendel anfängt zu glühen, dreht man das Schwungrad, bis der Motor ohne weitere Hilfe von selbst läuft.
Da die Spannung am Trafo und an der Heizwendel durch Spannungsverluste (z.B. am Abgreifer) unterschiedlich sind, mißt man die an der Wendel abfallende Spannung. Außerdem schaltet man ein Amperemeter in den Stromkreis, damit man so die Leistung der Heizwendel durch P = U I (P: Leistung; U: Spannung; I: Stromstärke) bestimmen kann.
Um die Drehzahl der Stirling-Maschine zu messen, wird die Lichtschranke eines Frequenzzählers an das Schwungrad angeschlossen.
Um den Motor unter Belastung auszumessen, wird ein sogenannter „Prony’scher Bremszaum“ verwendet. Man kann mit seiner Hilfe durch die Erhöhung der Reibung an der Achse die Belastung erhöhen.
Am Anfang wurde eine Heizspannung von U = 12,2 V angelegt und ein p-V-Diagramm (1) ohne Belastung bei f = 5,2 Hz gezeichnet. Danach wurde der Prony’sche Zaum angelegt und die Belastung durch Steigerung der Anpreßkraft der Backen erhöht. Um das durch die Reibung erzeugte Drehmoment auszumessen, wurde ein Kraftmesser im Abstand von l = (23 ± 0,2) cm angebracht und die Kraft notiert. Um den Prony’schen Zaum annähernd horizontal zu halten, wurden auf der anderen Seite bei Bedarf Gegengewichte (1 Gegengewicht: (0,5 ± 0,05) N) angebracht. Die Frequenz wurde im Bereich von 3,8 – 5,1 Hz variiert, und drei Messungen durchgeführt. Bei f = 4,2 Hz wurde nochmals (diesmal unter Belastung) ein p-V-Diagramm gezeichnet.
Nun wurde die Heizspannung auf U = 15,7 V erhöht. Es wurde wie oben verfahren, jedoch war es nicht möglich ein p-V-Diagramm des unbelasteten Motors zu zeichnen, da die Frequenz weit außerhalb des sicheren Bereiches war. Diesmal konnte die Frequenz von 4 - 6 Hz variiert werden.
| f [Hz] | U [V] | I [A] | W [J] | Geff [N] | M [Nm] | LH [W] | LM [W] | LP [W] | E [%] | hT [%] |
| 5,2 ± 0,2 | 12,2 ± 0,1 | 13,7 ± 0,1 | 3,27 ± 0,05 | 167,1 ± 1,9 | 17,0 ± 0,8 | 10,2 ± 0,5 | ||||
| 5,2 ± 0,2 | 12,2 ± 0,1 | 13,7 ± 0,1 | 3,62 ± 0,05 | 167,1 ± 1,9 | 15,2 ± 0,8 | 9,1 ± 0,5 | ||||
| 5,2 ± 0,2 | 12,2 ± 0,1 | 13,7 ± 0,1 | 1,2 ± 0,02 | 0,276 ± 0,021 | 167,1 ± 1,9 | 6,6 ± 0,7 | 3,9 ± 0,4 | |||
| 5,2 ± 0,2 | 12,2 ± 0,1 | 13,7 ± 0,1 | 0,43 ± 0,02 | 0,099 ± 0,021 | 167,1 ± 1,9 | 2,8 ± 0,7 | 1,7 ± 0,4 | |||
| 5,2 ± 0,2 | 12,2 ± 0,1 | 13,7 ± 0,1 | 0,25 ± 0,02 | 0,058 ± 0,021 | 167,1 ± 1,9 | 1,9 ± 0,7 | 1,1 ± 0,5 | |||
| 5,2 ± 0,2 | 15,7 ± 0,1 | 17,5 ± 0,1 | 4,34 ± 0,05 | 1,52 ± 0,02 | 0,350 ± 0,021 | 274,8 ± 2,4 | 8,8 ± 0,7 | 17,4 ± 0,9 | 3,2 ± 0,3 | 6,3 ± 0,4 |
| 5,2 ± 0,2 | 15,7 ± 0,1 | 17,5 ± 0,1 | 1,25 ± 0,02 | 0,288 ± 0,021 | 274,8 ± 2,4 | 8,1 ± 0,7 | 3,0 ± 0,3 | |||
| 5,2 ± 0,2 | 15,7 ± 0,1 | 17,5 ± 0,1 | 1,14 ± 0,02 | 0,262 ± 0,021 | 274,8 ± 2,4 | 8,4 ± 0,8 | 3,1 ± 0,3 | |||
| 5,2 ± 0,2 | 15,7 ± 0,1 | 17,5 ± 0,1 | 1,06 ± 0,02 | 0,244 ± 0,021 | 274,8 ± 2,4 | 8,4 ± 0,8 | 3,1 ± 0,3 | |||
| 5,2 ± 0,2 | 15,7 ± 0,1 | 17,5 ± 0,1 | 0,90 ± 0,02 | 0,207 ± 0,021 | 274,8 ± 2,4 | 7,8 ± 0,9 | 2,8 ± 0,4 |
Die Heizleistung und deren Fehler kann man durch
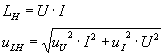
bestimmen.
Um die thermische Wirkungsgrad zu bestimmen, benötigt man zuerst die von der Maschine verrichtete Arbeit. Dies ist die Fläche innerhalb der geschlossenen p-V-Kurve (wegen dW = p dV). Diese Fläche bestimmten wir durch Auszählen der einzelnen Kästchen. Diese summierten wir dann zur Gesamtarbeit W. Den Fehler durch Auszählen und Ablesen konnten wir nur abschätzen (± 0,05 J). So wurde bei allen drei Graphen verfahren.
Der thermische Wirkungsgrad ht wurde durch:
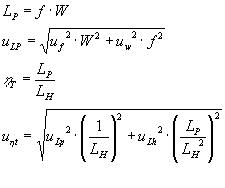
bestimmt.
Der effektive Wirkungsgrad he wurde durch
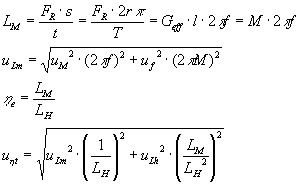
errechnet.
In Diagramm 1 bis 3 vermuten wir einen linearen Zusammenhang. Dies bestätigt sich in der Berechnung und Zeichnung einer Ausgleichsgeraden. Die doch vorhanden Abweichungen führen wir auf unruhigen Lauf sowie auf dauernd steigende Leistung (erwärmungsbedingt) des Stirling zurück.
In Diagramm 2 a, b wurde der effektive Wirkungsgrad gegen die Frequenz aufgetragen.
Der Wirkungsgrad sinkt um ungefähr 71% (a) bzw. 13% (b). Der innere Widerstand des Motors und seiner Bestandteile (wie z.B. Rhombengetriebe) bleiben auch bei erhöhter Frequenz in etwa gleich. Da der Motor aber die Kurve bei höheren Frequenzen nicht mehr so gut durchfahren kann, geht hier Leistung verloren.
Dazu muß man nun mechanische Arbeit leisten, die durch einen Elektromotor geliefert wird. Durch einen Keilriemen wird das Schwungrad des Kolbens im Uhrzeigersinn angetrieben.
Anstatt der Heizwendel wird nun ein kleines mit Wasser gefülltes Reagenzglas eingesetzt. Um die Temperatur zu messen, wird ein elektronischer Temperaturfühler in das Wasser gegeben. Danach startet man den Motor und mißt die Temperatur des Wassers in Abhängigkeit von der Zeit (in 15 s Schritten).
Man muß dazu nur die Laufrichtung des Schwungrads gegen den Uhrzeigersinn einstellen. Wieder mißt man die Temperatur des Wassers in Abhängigkeit der Zeit (in 15 Sekunden Intervallen). Der Knick im Graphen bei 450 s wurde dadurch hervorgerufen, daß wir das Reagenzglas weiter in die Maschine hineingeschoben haben, um die Heizgeschwindigkeit zu erhöhen.
In einem t-T-Diagramm kann man einen logarithmischen Anstieg/Abfall der Temperaturen erkennen.
Das Abflachen der Kurven ist damit zu erklären, daß das Verhältnis zwischen der zugeführten Energie der Stirling-Maschine und der Energieverlust an die Umgebung beinahe 1 ist. Auf einem halblogarithmischen Papier müßte man erkennen, daß die beiden Steigungen der Kurven dem Betrage nach gleich sind.