Trägheitsmoment (TRÄ)

Graphen

1 Einleitung

Die Drehbewegungen stellen in der Mechanik eine den geradlinigen Bewegungen äquivalente Erscheinung dar. Zum Verständnis von Drehbewegungen ist das Trägheitsmoment von großer Bedeutung. Es entspricht der Masse, die für die Trägheit eines Gegenstandes bei Bewegungsänderungen sorgt, denn es verhindert eine Änderung der Drehbewegung ohne einwirkendes Drehmoment, welches wiederum ein Äquivalent der Kraft darstellt.

Leider ist oft die theoretische Berechnung des Trägheitsmoments gerade für geometrisch komplexer aufgebaute Körper zu umfangreich bzw. nicht möglich.

In dem folgendem Versuch soll eine Möglichkeit, das Trägheitsmoment eines Körpers experimentell zu bestimmen, praktisch erprobt werden.

2 Theoretischer Hintergrund

2.1 Definition und Eigenschaften

Das Trägheitsmoment ist durch die Formel dJ = r² dm festgelegt, wobei dm einen winzigen Massenpunkt des Körpers und r der jeweilige Abstand des Massenpunktes dm von der Drehachse darstellt. Das Trägheitsmoment ist folglich für denselben Körper nicht immer gleich sondern variiert je nach der Lage der Drehachsen.

Ist das Trägheitsmoment eines Körpers bezüglich einer Achse durch den Schwerpunkt bekannt so ergibt sich für das Trägheitsmoment zu einer parallelen Achse nach dem Satz von Steiner: J = J_s + mr².

2.2 Drehschwingungen

Bei einer linearen Schwingung ohne Dämpfung gilt: F = -k * x , wobei F die rückstellende Kraft, k eine Konstante und x die Auslenkung aus der Ruheposition darstellt.  Ähnliches muß auch für eine Drehschwingung erfüllt sein: M = -D * j , hier ist M das rückstellende Drehmoment, D die Winkelrichtgröße und j die Winkelauslenkung. Solche Schwingungen findet man z.B. bei Drillfedern, nachdem sie aus ihrer Ruhelage ausgelenkt wurden. Analog zu normalen Schwingungen erhält man die Schwingzeit zu :

T = 2p (J/D)^1/2. Daraus läßt sich bei bekannter Schwingungszeit das Trägheitsmoment J ermitteln. Oft ist jedoch in der Praxis die Winkelrichtgröße eines Drehschwingsystems nicht bekannt und muß erst über die Messung des wirkenden Drehmoments bei einem bestimmten Winkel berechnet werden: D = -M/j.  Bringt man einen Gegenstand mit bekannten Trägheitsmoment J₁ an, so läßt sich aus der Schwingungszeit der unbeschwerten Drillachse T_u = 2p (J/D)^1/2 und der beschwerten T₁ =2p (J/D)^1/2 die Konstante D = 4p²J₁/(T₁-T_u) ermitteln.

3 Experiment

3.1 Bestimmung des Trägheitsmoments einer menschenähnlichen Puppe

3.1.1 Bestimmung von D mit Drehmomentsmessung

Es standen uns ein Drehteller mit unbekannter Federkonstante D und Trägheitsmoment J zur Verfügung. Zuerst brachten wir eine Stange mit Öse an und maßen den Abstand d von der Öse zur Drillachse, wobei sich mit Hilfe eines Kraftmessers das angreifende Drehmoment errechnen ließ. Die Kraft wurde bei vier Auslenkungswinkeln festgehalten.

Mit D* = F*d/j (j in rad) erhielten wir folgendes

3.1.2 Bestimmung von D (zweite Methode)

Da das Trägheitsmoment der Drillachse unbekannt war, brachten wir an einer Trägheitsstange zwei Metallzylinder Z₁ und Z₂ an, deren Trägheitsmoment J_Z wir uns mit Hilfe der Formel J_s = m(r²/4 + l²/12 + R²), (R: Abstand des Schwerpunktes zur Drehachse (Satz von Steiner)) ausrechneten.

An den zur Verfügung gestellten Gegenständen ließen sich untenstehende Werte feststellen:

	Masse m/kg	Länge l/m	Radius r/m
Trägheitsstange	0,023	0,420	0,0015
Zylinder	0,061	0,010	0,015

	Befestigungsposition R/m	T/s	J/Nm
Messung 0		0,78	6,9 * 10 -5
Messung 1	0,100	1,60	2,8 * 10 -4
Messung 2	0,205	2,98	6,7 * 10 -4

Der Fehler der gemessenen Werten liegt jeweils bei ± 1 der letzten angegebenen Stelle.

Damit ergibt sich die Winkelrichtgröße nach D* = 4p²J₁/(T₁²-T_u²); T_u ist die Schwingzeit der unbelasteten Drillachse. Daraus erhielten wir einen Wert für von D* = (23,8 ± 1,3) 10^-3 Nm.

3.1.3 Trägheitsmoment der Puppe

Die Puppe wurde auf der Drillachse befestigt und die Schwingachse für zwei Positionen festgehalten - einmal mit angelegten und dann mit ausgestreckten Armen. Durch Messen der Schwingungszeit kann man so das Trägheitsmoment des gesamten Systems errechnen. Um jedoch nur das Trägheitsmoment der Puppe zu erhalten, muß noch das Trägheitsmoment der Drillachse abgezogen werden.

Es ergibt sich somit ein Verhältnis von
J_ang / J_aus = 0,24 ± 0,06

3.2 Bestimmung des Trägheitsmoments eines Menschen

3.2.1 Bestimmung der Winkelrichtgröße des großen Drehtellers

An einem großen Drehteller wurden mit einer Federwaage die auftretenden tangentialen Kräfte in 10°-Schritten gemessen und so das rücktreibende Drehmoment bestimmt.

Bei der graphischen Auswertung bemerkt man, daß das rückstellende Drehmoment nicht exakt linear verläuft, sondern leicht gekrümmt ist. Man legt daher graphisch eine Ausgleichsgerade durch die einzelnen Messungen.

Wir erhielten mit

D* = F * r / j

einen graphischen Mittelwert von:

D* = (1,870 ± 0,022) Nm (bestimmt durch Fehlerrechnungsprogramm von Johannes Vrana)

3.2.1.1 Trägheit der Apparatur und von Daniel

Zur Bestimmung des Trägheitsmoments der Drehtellerapparatur haben wir die Schwingungszeit ohne zusätzliche Gewichte gemessen. Um die Schwingungszeit genauer messen zu können, haben wir die oben erwähnte Lichtschranke auch an diesen Drehteller „angeschlossen“.

Danach haben wir uns (analog zu den Haltungen der Puppe) auf den Teller gestellt und wieder die entsprechenden Schwingungszeiten gemessen. (Exemplarisch sei hier mit den Werten von Daniel Dolinsky gerechnet)

Durch folgende Formel:

J_Daniel = D^* * (T² - T_u² ) / (4 * p²)    T_U=(3,5 ± 0,1) s

errechneten wir

und damit ein Verhältnis von:

J_ang / J_aus = 0,664 ± 0,021

3.2.2 Theoretische Berechnung des Trägheitsmoments von Daniel

3.2.2.1 Der Mensch als Zylinder

Wäre Daniel ein Zylinder, könnte man aus Masse, Höhe und Dichte das Trägheitsmoment bezüglich der Achse berechnen:

J = m²/(2prh) = 0,44 kg m²

Der Wert von 0,664 kg m² ist recht unsicher und der gerade errechnete Wert gilt eben nur für einen zylindrischen Körper.

Puppe ® Mensch

Um die Trägheit des Menschen aus dem Modell der Puppe zu ermitteln, verwendet man

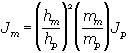
als Beziehung zwischen den Trägheitsmomente der Puppe und des Menschen. Daraus ergibt sich

 J_m,angelegt = 0,81 kg m²  J_{m,ausgestreckt} = 3,36 kg m²

Den nicht unwesentlichen Abweichungen von den experimentell bestimmten Werten liegt abermals die Modellvorstellung zugrunde. Das Verhältnis der Puppe zu Daniel muß nicht die vorausgesetzten Bedingungen erfüllen.

4 Theoretische Bestimmung der Trägheit

Um das Modell vom großen Zylinder zu verfeinern, teilt man den Körper der Puppe und des Menschen in mehrere geometrische Körper ein, von denen man jeweils das Trägheitsmoment weiß und noch mit dem Steinerschen Satz dessen Trägheitsmoment zur Drehachse errechnen kann.

Zuvor muß man alle Körperteile der Puppe bzw. von Daniel ausmessen.

Danach kann man mit den errechneten Maßen und einer festen Masseverteilung für die einzelnen Gliedmassen das dazugehörige Trägheitsmoment.

Für ausgestreckte Arme das Zylinder-Modell wie folgt verfeinern:

   Zusätzliches Trägheitsmoment des Zylinderpaares ausgestreckte Arme: 2,55 kg m²

   zusätzliches Trägheitsmoment des Zylinderpaares angelegte Arme: 1,7 kg m²

Als sehr problematisch zeigt sich die Messung des Abstandes der Arme und Beine von der Drehachse. Auch die Lage von Daniel Körper auf dem Drehteller beeinflußt diesen Wert.  Ist Daniel nicht vollkommen senkrecht und zentral auf dem Drehteller, so ändert sich der Wert des Trägheitsmoments zum Teil recht erheblich, da eine Verlegung des Körperschwerpunktes aus der Drehachse heraus mit dem Satz von Steiner schwerwiegende folgen hat. Dies verursacht eine Abweichung von an die 0,2 bis 0,8 kg/m² bei Abweichungen von 5 bzw. 10 cm von der Drehachse, welches schon in der Größenordnung des Ergebnisses liegt.

Bei diesem großen Fehler ist es auch nicht mehr sehr sinnvoll das Modell verbessern zu wollen, da im Großen und Ganzen die erhaltenen Volumen mit der angegebenen Massenverteilung recht gut übereinstimmen.

5 Fragen

5.1

cos a =F_senkrecht/F_zug Þ (F_zug - F_senkrecht) / F_zug = 1-cos a

a = 5° Þ relativer Fehler ist 0,38 %

a = 10° Þ relativer Fehler ist 1,52 %

5.2

J_versetzt = J_p + m r² = 0,78 kg m²

5.3

(J_Z-J_m) / J_Z = m (r²/4 + h²/12 + d² - d²)/( m (r²/4+h²/12+d²)) =  (r²/4 + h²/12)/ (r²/4+h²/12+d²) = 0,62 %

5.4

Man bestimmt das Verhältnis x der Amplitude u einem Zeitpunkt und einer Periode später. Es gilt:

t_b = t_a + 2p/w, y_a = y_0exp((iw-d)t_a), y_b = y₀exp((iw-d)t_b) = y₀exp(iwd_a-dt_b), x = y_a/y_b = exp(d(t_b-t_a)) = exp(2dp/w),

ln x = 2pd/w, d = (w ln x) / (2p), w₀²=w² + d² = w(1+(ln x)²/(4p²)), w₀ = w(1+(ln x)²/(4p²))^1/2,

t₀ = t/(1 + (ln x)² / (4p²))^1/2.

Die Periodendauer ohne Dämpfung ist also stets kleiner als mit Dämpfung.

Der Ausdruck des T-Y-Schreibers zeigt kaum ein exponentielles Abfallen der Amplitude. Das Verhältnis der Amplitude nach keiner, einer halben, ganzen bzw. eineinhalbfachen Schwingung zur anfänglichen Amplitude beträgt 1, 7/12, 5/15 bzw. 0.  Man kann das Amplitudenverhältnis in einer Periode auf ca. 3-4 schätzen.  Nach der oben ermittelten Formel kann man den relativen Fehler der Periode mit x = 3 bzw. 4 auf ca. 1,5 % - 2,5 % errechnen, also ist trotz der starken Dämpfung kein großer Fehler der Meßwerte zu erwarten.

5.5

Zylinder: J = m² /(2prh)

elliptischer Zylinder:

m = rh2pr²

r² = ½ m/(prh)

J_e = ¼ m (r² + 4 r²) = 5/4 m r² = 5/8 m² / (prh) = 5/4 m²/ (2prh) = 5/4 J

Das Trägheitsmoment des elliptischen Zylinders ist um 25 % größer.