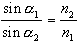 ,
,Einfachspalt: sin(a) über Ordnungszahl
Gitter: sin(a) über Ordnungszahl
Brechung: Wellenlänge über Brechungszahl
Excel-Tabelle mit der alles berechnet wurde
Die geradlinige Ausbreitung des Lichts gilt nicht mehr, wenn das Licht auf ein Objekt, wie zum Beispiel Gitter oder Spalt trifft. Falls das Objekt oder der Spalt in der Größenordnung der Wellenlänge des Lichts liegt, bestimmt die Wellennatur des Lichtes die weitere Ausbreitung. Nach dem Huygenschen Prinzip entsteht an jedem Punkt der Öffnung eine neue Elementarwelle, die sich auch in den geometrischen Schattenbereich ausbreitet und mit den anderen Wellen Minima und Maxima bilden.
Diese Interferenz kommt dadurch zustande, daß je nach Gangunterschied sich die Wellen gegenseitig auslöschen oder verstärken. Daher sind diese Extrema auch von der Wellenlänge abhängig.
Im Gegensatz dazu läßt sich die Brechung auch noch ohne Verwendung der Welleneigenschaft des Lichts erklären. Wenn der Lichtstrahl auf eine ebene Grenzfläche zwischen 2 Medien mit verschiedener Ausbreitungsgeschwindigkeit des Lichtes trifft, erfährt es eine Brechung.
nach Snellius gilt:
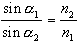 ,
,
wobei a1 der Einfallswinkel gegen das Lot auf die Ebene und a2der Ausfallswinkel ebenfalls gegen das Lot, und n1, n2 die verschiedenen Brechungsindexe der Medien sind.
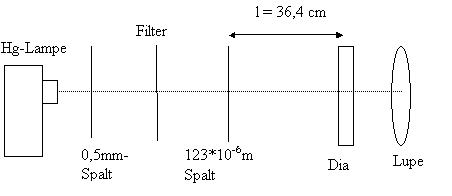
Das Licht einer Hg-Lampe wird durch einen Spalt geschickt, um zu gewährleisten, daß am 2. Spalt das Licht parallel auftrifft. Die Hg-Lampe sendet im Wesentlichen drei sichtbare Wellenlängen aus. Um ein Interferenzmuster betrachten zu können, müssen bis auf eine (hier die Grüne) alle anderen Wellenlängen ausgeblendet werden. Dies geschieht durch einen Grünfilter.
Danach trifft das Licht auf ein Dia, in das eine Millimeterskala eingezeichnet ist. Durch die Lupe kann man so relativ genau die Abstände der Interferenzmaxima und -minima gleicher Ordnung mehrfach ablesen.
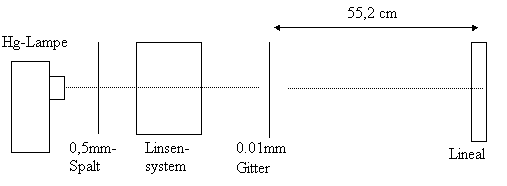
Bei der Beugung am Gitter bleibt im Wesentlichen der Versuchsaufbau erhalten. Genau wie beim Einfachspalt wird durch den ersten Spalt die Parallelität des Strahlenbündels erreicht. Das Linsensystem ermöglicht eine scharfe Abbildung auf das Lineal. Durch die Beugung am Gitter entstehen scharfe Maxima auf dem Lineal. Der Abstand des Lineals wird so eingestellt, daß in etwa je 3 Maxima von den verschiedenen Wellenlängen (lila, grün, gelb) darauf abgebildet werden. Man liest dann mehrfach den Abstand der Maxima ab.
Wir ermittelten die Wellenlänge des grünen Lichts sowohl rechnerisch als auch graphisch. Durch die Formeln auf Seite 8 im Skript erhält man dann die Wellenlänge und den dazugehörigen Fehler.
l = 577 ± 8 nm
Um l graphisch ermitteln zu können, errechneten wir die Werte von sin a.
Danach trugen wir die Werte noch in einen n-sin a -Graphen ein (Ordnung-sin) und legten rechnerisch (Computerprogramm von Johannes Vrana) eine Ausgleichsgerade durch die Punkte.
Der Ziel dieses Versuchs war ebenfalls die Wellenlängenbestimmung, diesmal aber von allen drei Farben.
Dazu errechneten wir durch die Formel auf Seite 5 im Skript jeweils die Wellenlängen der einzelnen Linien.
lGelb = (597 ± 17)nm
lGrün = (562 ± 17)nm
lBlau = (446 ± 6)nm
Das dritte Maximum war scheinbar zu schwach (beleuchtungsbedingt), deshalb nahmen wir hier nur die vierte Linie auf.
Anschließend ermittelten wir noch die sin a - Werte und trugen diese dann gegen die Ordnungszahl in ein Diagramm ein. Wir errechneten die Ausgleichsgrade und ermittelten aus deren Steigung ebenfalls die Wellenlängen.
Die von uns errechneten Wellenlängen sind leider immer über den Werten in der Literatur (hier: Bergmann-Schäfer, gelb: 577 nm; grün: 546,1 nm; blau: 435,8 nm).
Als Erklärung bleiben uns nur systematische Fehler, z.B. Gitterkonstante kleiner als angegeben.
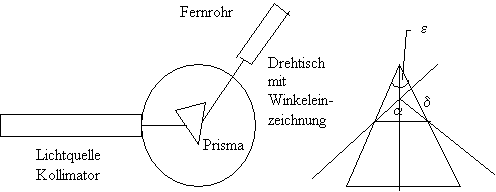
Nach Scharfstellung des Spalts mit dem Fernrohr, wurde der Winkel des Prismas e wie folgt gemessen:
Man bringt das Prisma so in den Strahlengang, daß es möglichst symmetrisch zu diesem ist. Dann mißt man die Winkel auf der eingezeichneten Skala. Dabei gilt:
e = a/2 = 60° ± 0,1°.
Danach wurde für jede Wellenlänge dmin (der Winkel der kleinsten Ablenkung, d.b. einen symmetrischen Strahlenverlauf durch das Prisma) ermittelt, indem man mit dem Fernrohr den jeweiligen Linien folgt, während das Prisma langsam gedreht wird. Beim Umkehrpunkt der Bewegung der Linien ist dann dieser Winkel erreicht. Die Werte der Winkel waren folgende:
dmin (gelb) = 30,2° ± 0,2°
dmin (grün) = 31,2° ± 0,2°
dmin (blau) = 33,2° ± 0,2°
Daraus lassen sich dann die Werte für den Brechungsindex durch
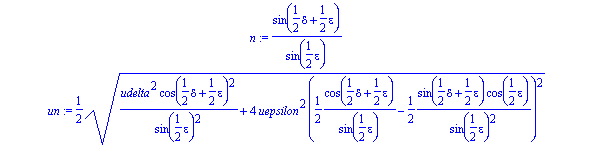
ausrechnen.
n(gelb) = 1,417 ± 0,004
n(grün) = 1,429 ± 0,004
n(blau) = 1,453 ± 0,004
Wir haben dann die Werte in einen Graphen eingetragen. Wir vermuteten aufgrund von n-l-Graphen in der Literatur einen nichtlinearen Zusammenhang zwischen der Wellenlänge und dem Brechungsindex.
Am besten lassen sich Interferenzerscheinungen durch eine monochromatische Lichtquelle erreichen, da sonst Interferenzen verschiedener Wellenlängen auftreten und sich die Maxima und Minima überschneiden.
Außerdem muß die Phasendifferenz der Lichtquelle zeitlich konstant sein, also kohärent.
2. Beugung tritt an jeder Kante auf, aber nur für kleine Spalten kann eine gute Interferenz beobachtet werden.
Lichtgeschwindigkeit:
cGlas = cVak /nglas
c(gelb) = 1,84*108 m/s
c(grün)= 1,83*108 m/s
c(gelb)= 1,82*108 m/s
Dispersion ist die Abhängigkeit des Ausbreitungsgeschwindigkeit in einem Medium von der Wellenlänge.
Die Auflösung wird durch Beugungserscheinungen, Spaltbreite bzw. durch nicht ganz exakte Geräte eingeschränkt.
l nimmt vom Roten zum Blauen zu
n(gelb) < n(grün) < n(rot)
Wie schon oben erwähnt kann man aus drei Werten nicht viel schließen, aber es ist anzunehmen, daß der Verlauf nicht linear ist, sondern n proportional zu 1/l ist.